-
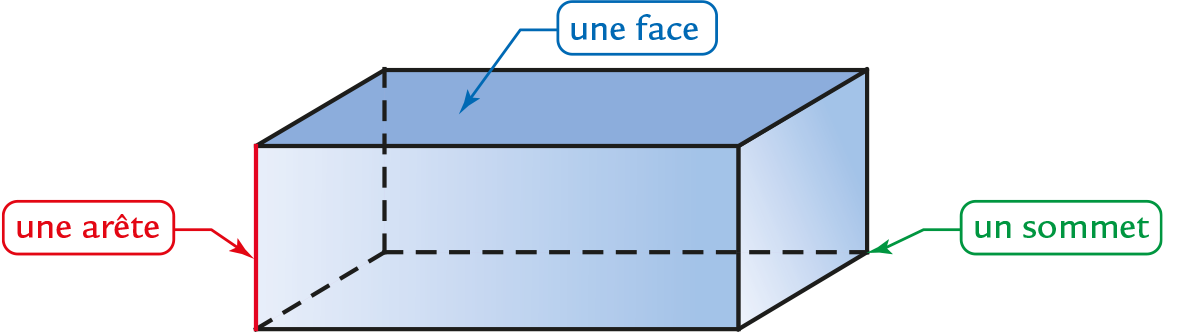
Parallélépipède rectangle
Définition

Un parallélépipède rectangle (ou pavé droit) est un solide qui possède six faces, toutes des rectangles.
Propriété
Un parallélépipède rectangle a 6 faces, 8 sommets et 12 arêtes.
-
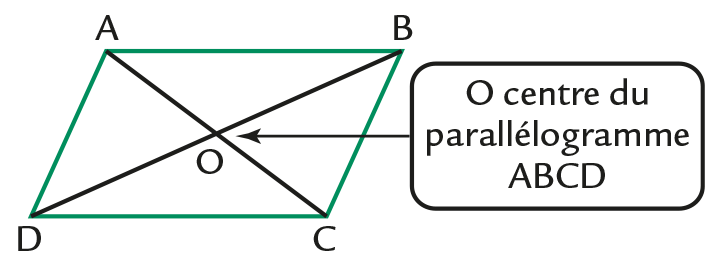
Parallélogramme
Définition

Un parallélogramme est un quadrilatère qui a un centre de symétrie.
Le centre de symétrie est appelé centre du parallélogramme (point d’intersection de ses diagonales).
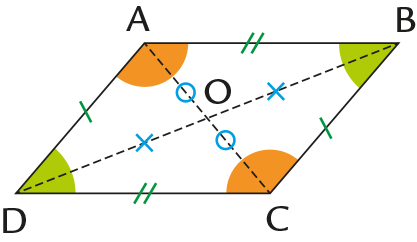
Propriétés

Si un quadrilatère est un parallélogramme, alors :
● ses diagonales ont le même milieu ;
● ses côtés opposés sont parallèles deux à deux ;
● ses côtés opposés sont de même longueur ;
● ses angles opposés sont égaux.
Remarque
Si un quadrilatère possède une de ces propriétés, alors c’est un parallélogramme.
-
Patron d’un solide
Définition

Le patron d’un solide est une figure qui permet, après découpage et pliage, de fabriquer ce solide sans que deux faces ne se superposent.
Exemple
On peut fabriquer un parallélépipède rectangle à partir d’un patron.
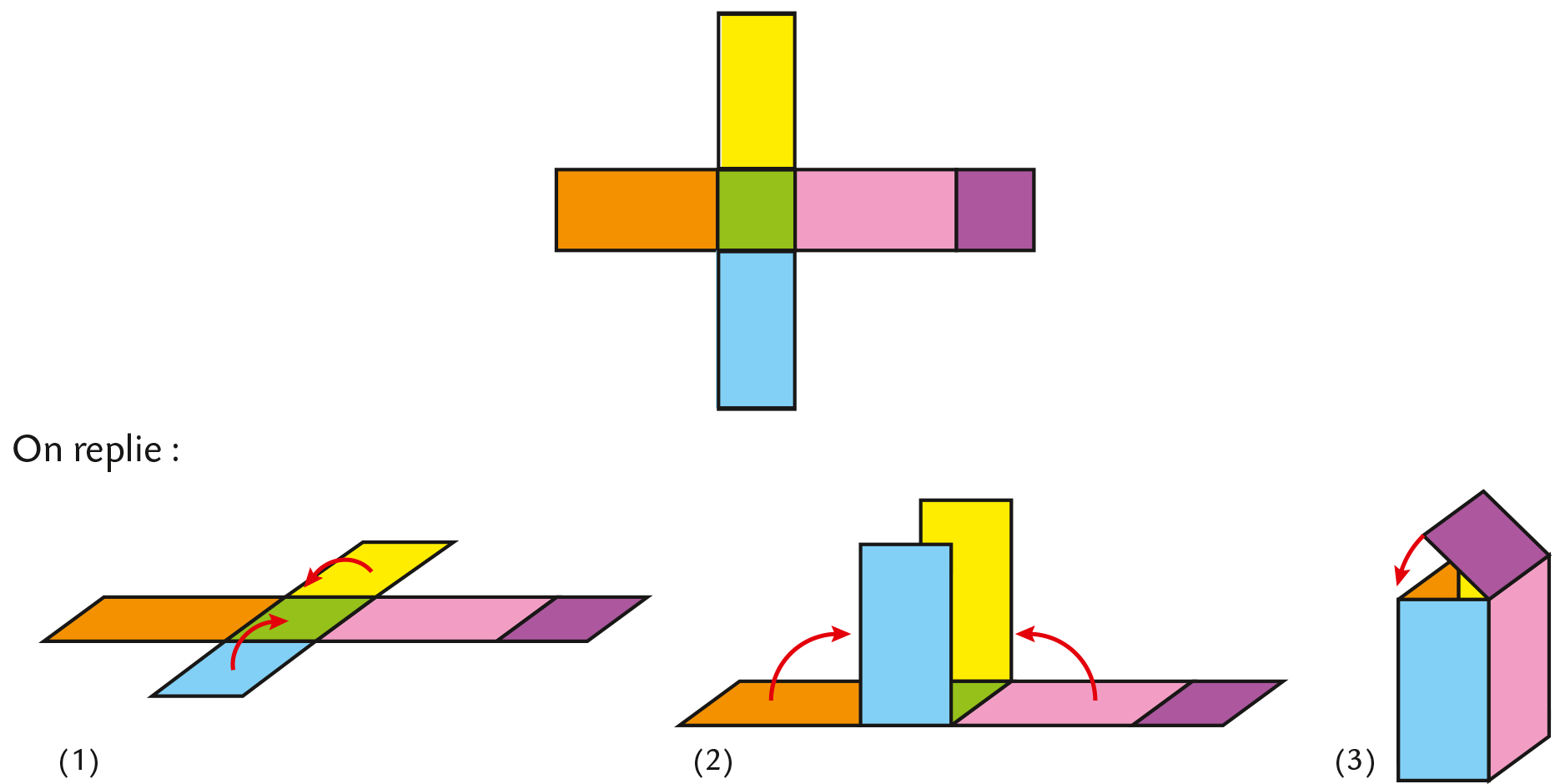
-
Pavé droit
Définition

Un parallélépipède rectangle (ou pavé droit) est un solide qui possède six faces, toutes des rectangles.
Propriété
Un parallélépipède rectangle a 6 faces, 8 sommets et 12 arêtes.

-
Périmètre
Définition

● Le périmètre d’une figure plane est la longueur du contour qui la délimite.
● L’aire d’une figure plane est la mesure de sa surface intérieure. Elle est délimitée par son contour.Exemple
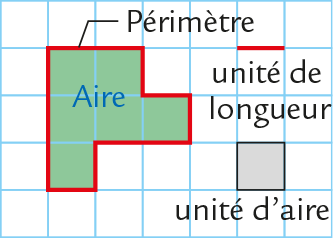
Remarque

L’aire et le périmètre d’une figure ne varient pas toujours dans le même sens.
Par exemple, l’aire de la figure (1) est plus grande que l’aire de la figure (2) mais le périmètre de la figure (1) est plus petit que le périmètre de la figure (2).
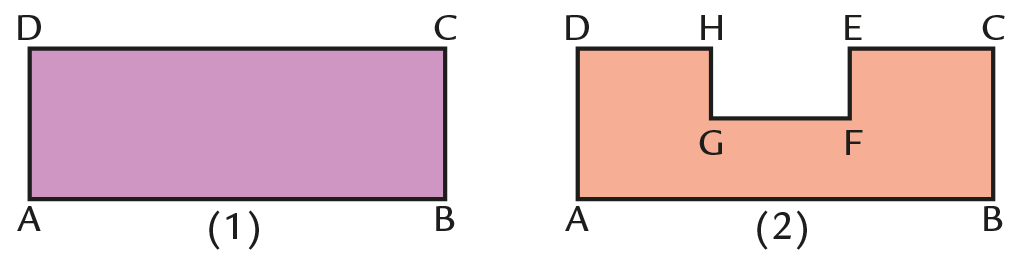
-
Périmètre d’un cercle
Propriété

Pour calculer le périmètre \({\cal P}\) d’un cercle de rayon \(\mathcal r\), on applique la formule :
\({\cal P} = 2 \times \pi \times r\) ou \({\cal P} = \pi \times d\) (où \(d = 2 × r)\).
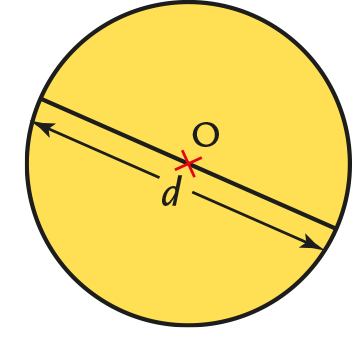
Exemple
Le périmètre d’un cercle de diamètre 5 cm est (en cm) :
\({\cal P} = 5 × π\)
\({\cal P} \approx 15,7\)
-
Périmètre d’un polygone
Propriété

Pour calculer le périmètre \(\mathcal P\) d’un polygone, on additionne les longueurs de ses côtés.
Exemple
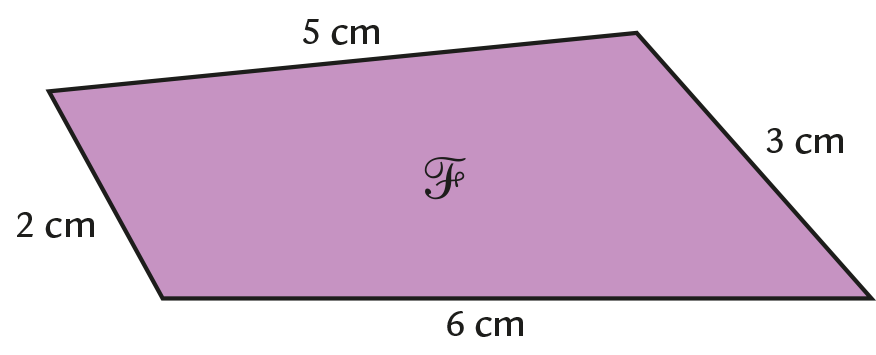
\(\mathcal P = 5 + 3 + 6 + 2 = 16\)
La figure \(\mathcal F\) a pour périmètre 16 cm.
Propriétés

● Le périmètre \(\mathcal P\) d’un carré de côté \(\mathcal c\) est donné par la formule \({\cal P} = 4 × c\).
● Le périmètre \(\mathcal P\) d’un rectangle de longueur L et de largeur \(\ell\) est donné par la formule \(\mathcal P = (\)L \(+\) \(\ell) \times 2\).
-
Perspective cavalière
Propriétés

Dans le dessin en perspective cavalière d’un parallélépipède rectangle (à l’échelle 1) :
● les faces avant et arrière sont des rectangles et elles gardent leurs dimensions ;
● les arêtes qui sont parallèles dans la réalité sont représentées par des segments parallèles ;
● les dimensions des arêtes fuyantes sont réduites par rapport aux dimensions réelles ;
● les arêtes cachées sont tracées en pointillés.
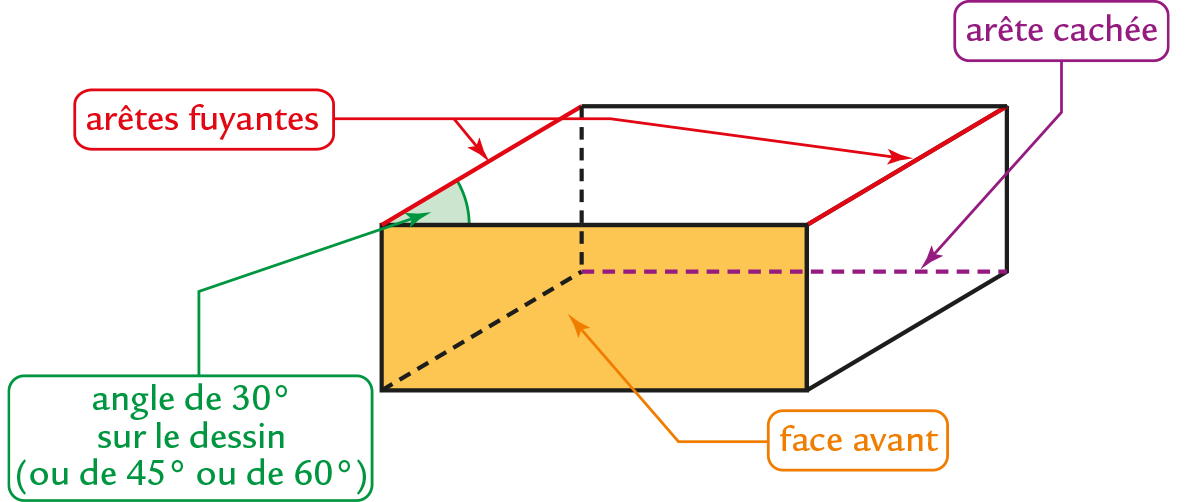
Remarque
Les angles droits de l’objet réel ne sont pas tous représentés par des angles droits en perspective cavalière.
-
Population
Définitions

● Les valeurs d’une série statistique se rapportent à une population et un caractère donnés.
La population représente l’ensemble des « individus » de la série.
Le caractère désigne la « qualité » étudiée chez ces individus.
● Un caractère est quantitatif quand ses valeurs sont des nombres.
Un caractère est qualitatif quand ses valeurs ne sont pas des nombres.Exemples
● On relève les notes obtenues à un contrôle commun par les élèves de 5e d’un collège.
La population est l’ensemble des élèves de 5e du collège.
Le caractère étudié est la note obtenue au contrôle commun : 7, 8, 9, 10, 11, 12, 13, 14, 15, etc. ; c’est un caractère quantitatif.
● On demande aux élèves d’une classe de 5e les pays d’Europe qu’ils ont visités.
La population est les élèves de la classe de 5e.
Le caractère étudié est les pays d’Europe visités : Italie, Espagne, Pologne, Angleterre, etc. ; c’est un caractère qualitatif. -
Pourcentage
Propriété

\(\mathcal p\) désigne un nombre positif.
Calculer \(\mathcal p\) % d’un nombre, c’est multiplier ce nombre par \(\dfrac{p}{{100}}\).Remarques
● Un pourcentage est un nombre qui représente un coefficient de proportionnalité.
● « 100 % d’un nombre » est égal à ce nombre.
● « 50 % d’un nombre » est égal à la moitié de ce nombre.Exemple
Pour calculer 5 % de 320, on effectue :
\(\dfrac{5}{{100}} × 320 = 0,05 × 320 = 16\)
-
Préfixes des unités de mesure
Définition

Les préfixes désignent des multiples et des fractions de 10 ou de 1 000 de l’unité.
On les utilise pour manipuler plus facilement de très grands ou de très petits nombres d’unité de mesure.
Exemples
● 1 giga vaut 1 000 000 000 ou 109 : 1 GW = 109 W.
● kilo (k) signifie 1 000 : 1 kg = 103 g = 1 000 g.
● 1 hL = 10² L = 100 L
● 1 mg = 10–3 g = 0,001 g
● 1 nm = 10–9 m -
Priorités opératoires
Propriété

Dans un calcul sans parenthèses et formé uniquement d’additions et de soustractions, on effectue les calculs de gauche à droite.
Exemple
\(A = 58 − 7 + 3\)
\(A = 51 + 3\)
\(A = 54\)Propriété

Dans un calcul sans parenthèses, on effectue les multiplications et les divisions en priorité sur les additions et les soustractions.
Exemples
●
\(B = 31\)
●
\(C = 30\)Propriété

Dans un calcul avec parenthèses, on effectue en priorité les calculs entre parenthèses.
Remarque
Quand les calculs entre parenthèses sont achevés, ces parenthèses disparaissent.
Exemples
●
\(D = 12\)
●
\(E = 18 − 10\)
\(E = 8\)Propriété

Dans un calcul sans parenthèses, on effectue en priorité les carrés, puis les multiplications et les divisions et enfin les additions et les soustractions.
Exemple
\(F = 50\;– 6 − 9\)
\(F = 44 − 9\)
\(F = 35\) -
Prisme droit
Définitions

● Un prisme droit est un solide dont :
– deux faces superposables et parallèles sont des polygones (triangle, quadrilatère quelconque, rectangle, parallélogramme…). Ces faces sont appelées bases du prisme ;
– les autres faces sont des rectangles. On les appelle faces latérales.
● La distance entre les deux bases est appelée hauteur du prisme.
Exemples
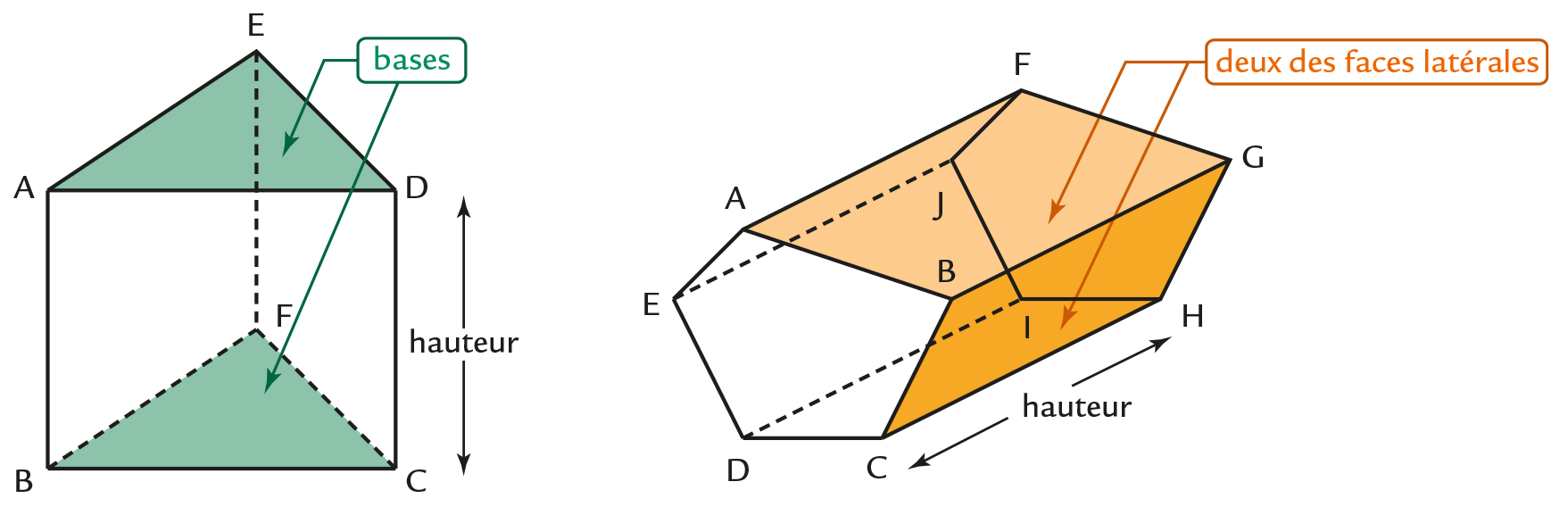
Remarque
Un parallélépipède rectangle est un prisme droit dont les bases sont des rectangles.
-
Probabilité
Définition

Pour certaines expériences aléatoires, on peut déterminer par un quotient la « chance » qu’un évènement a de se produire. Ce quotient est appelé probabilité de l’évènement.
Exemple
Si on tire au hasard une boule dans un sac contenant huit boules dont trois sont rouges et cinq sont vertes, la probabilité de tirer une boule rouge est de \(\dfrac{3}{8}\), car on a 3 « chances » sur 8 de tirer une boule rouge.
Propriété

Si on répète une expérience aléatoire un très grand nombre de fois, la fréquence de n’importe quel évènement de cette expérience finit par se stabiliser autour d’un nombre qui est la probabilité de cet évènement.
Exemple
Expérience : « On dispose d’un sac qui contient 3 boules bleues et 4 boules vertes. On tire une boule au hasard et on s’intéresse à la couleur de la boule tirée. »
Si on renouvelle un très grand nombre de fois cette expérience, en remettant chaque fois la boule tirée dans le sac, la fréquence du résultat « la boule est bleue » se stabilise autour de \(\dfrac{3}{7}\) qui est la probabilité de l’évènement « Obtenir une boule bleue ». -
Probabilité d’une issue
Définitions

Une expérience est dite « aléatoire » si elle vérifie deux conditions :
● elle conduit à des résultats possibles, appelés issues, qu’on est parfaitement capable de nommer ;
● on ne sait pas lequel de ces résultats va se produire quand on réalise l’expérience parce que le résultat est déterminé par le hasard.Remarque
Une expérience aléatoire doit être reproductible dans les mêmes conditions.
Exemples
● Expérience (A) : « On lance une pièce de monnaie et on regarde sur quelle face elle tombe. »
Cette expérience est bien une expérience aléatoire car :
- il y a deux issues possibles : « pile » ou « face » ;
- quand on lance la pièce, on ne sait pas sur quelle face elle va tomber.
● Expérience (B) : « On place de l’eau à une température de –15 °C. »
Cette expérience n’est pas aléatoire car on sait que l’eau va se transformer en glace.Propriétés

● La probabilité d’une issue est un nombre compris entre 0 et 1.
● La somme des probabilités de toutes les issues d’une expérience aléatoire est égale à 1. -
Probabilité d’un évènement
Définition

Dans une expérience aléatoire, les évènements sont des ensembles de résultats de cette expérience.
Un évènement, s’il est réalisé, est constitué d’une ou plusieurs issues.Exemple
Expérience aléatoire : « Lancer d’un dé à 6 faces numérotées de 1 à 6. »
● « Obtenir un nombre pair » est un évènement car c’est l’ensemble des résultats suivants :
« Obtenir un 2 » ou « Obtenir un 4 » ou « Obtenir un 6 » ; il est donc réalisé par trois issues.
● « Obtenir un 3 » est aussi un évènement, réalisé par une seule issue.
● « Obtenir un nombre supérieur à 5 » est aussi un évènement, réalisé par une seule issue (« Obtenir un 6 »).Propriétés

● Quand les résultats d’une expérience aléatoire ont tous la même probabilité, alors la probabilité d’un évènement est égale au quotient :
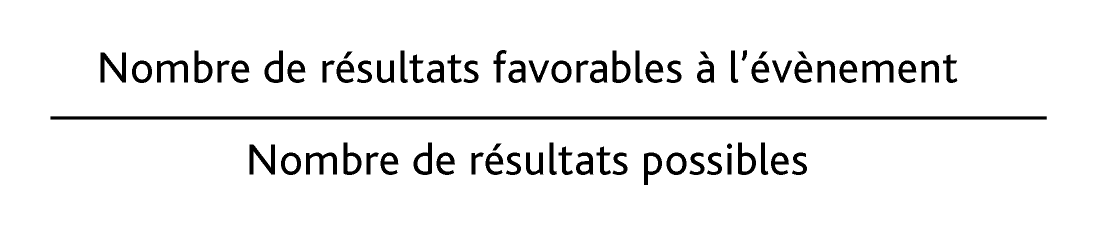
● La probabilité d’un évènement réalisé par plusieurs issues est la somme des probabilités de chacune de ces issues.
● La probabilité d’un évènement est toujours comprise entre 0 et 1.Exemple
Expérience : « On lance un dé à 6 faces numérotées de 1 à 6. Quelle est la probabilité d’obtenir un nombre inférieur à 5 ? »
Les résultats (« Obtenir un 1 », « Obtenir un 2 », …, « Obtenir un 6 ») de cette expérience ont la même probabilité. Il y a 6 résultats possibles.
Les résultats favorables à l’évènement « Obtenir un nombre inférieur à 5 » sont : « Obtenir 1 ; 2 ; 3 ou 4 ». Donc le nombre de résultats favorables est 4.
Donc la probabilité de l’évènement « Obtenir un nombre inférieur à 5 » est \(\dfrac{4}{6}\). -
Produit
Définition

Le résultat d’une multiplication est appelé un produit.
\(a × b\) est le produit de \(\mathcal a\) et de \(\mathcal b\).Exemple
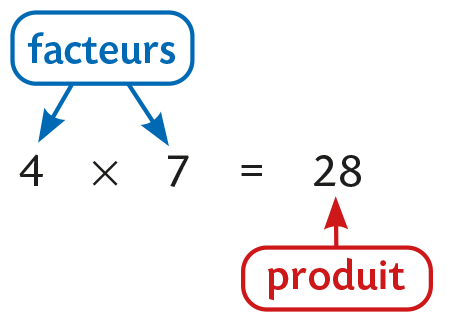
-
Produits en croix
Définition

Quels que soient les nombres \(\mathcal a\), \(\mathcal b\), \(\mathcal c\) et \(\mathcal d\) (avec \(\mathcal b\) ≠ 0 et \(\mathcal d\) ≠ 0) :
• si \(\dfrac{a}{b} = \dfrac{c}{d}\) alors \(a × d = b × c\).
• si \(a × d = b × c\) alors \(\dfrac{a}{b} = \dfrac{c}{d}\).Exemples
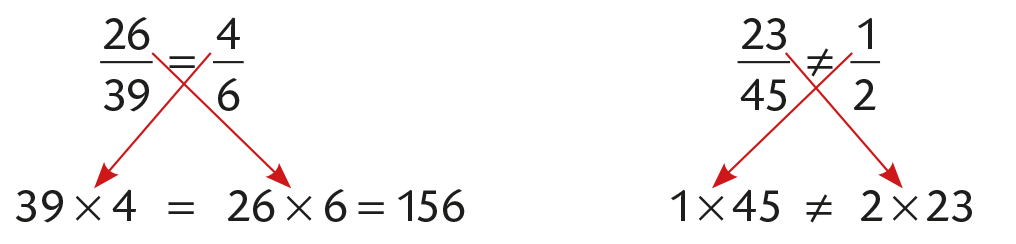
-
Programmation
Définitions

● L’algorithmique est la méthode qui vise à créer des algorithmes, c’est-à-dire à déterminer les différentes étapes et actions à mettre en place pour répondre à un problème donné.
● La programmation est la traduction de ces étapes et actions dans un langage compréhensible par un ordinateur : le langage de programmation. -
Proportionnalité
Propriété

On peut représenter deux grandeurs proportionnelles dans un tableau de proportionnalité, dans lequel les lignes (ou colonnes) sont proportionnelles entre elles : les nombres d’une ligne peuvent être calculés en multipliant (ou en divisant) les nombres de l’autre ligne par un nombre, toujours le même. Ce nombre est appelé coefficient de proportionnalité.
Remarque
Pour vérifier qu’un tableau est un tableau de proportionnalité ou pour compléter un tableau de proportionnalité, on peut utiliser l’égalité des produits en croix.
Exemples
● Le tableau suivant est un tableau de proportionnalité.
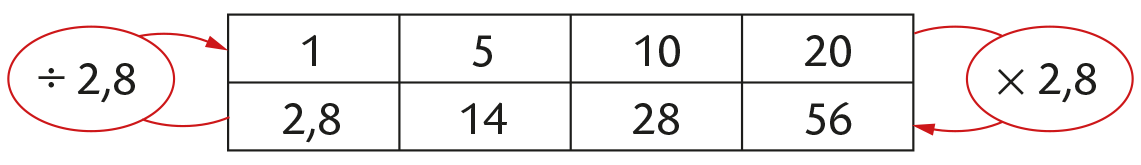
Le coefficient de proportionnalité est 2,8.
● La quantité d’essence achetée et le prix payé sont proportionnels car, pour trouver le prix payé, on multiplie la quantité achetée par le prix d’un litre.
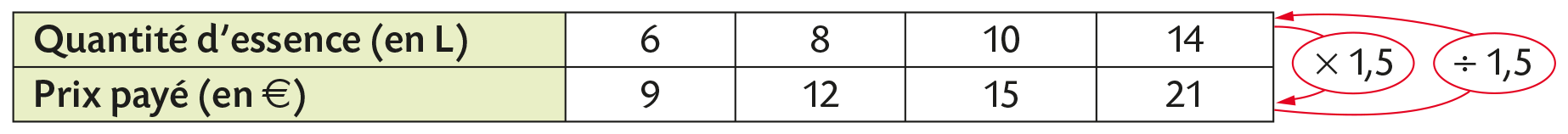
\(\dfrac{9}{6} = 1,5\;;\;\dfrac{{12}}{8} = 1,5\;;\;\dfrac{{15}}{{10}} = 1,5\;;\;\dfrac{{21}}{{14}} = 1,5\) donc c’est bien un tableau de proportionnalité.
Dans cet exemple, un coefficient de proportionnalité est le prix d’un litre d’essence (en €).Propriété

On peut représenter graphiquement deux grandeurs proportionnelles : on obtient alors des points alignés sur une droite qui passe par l’origine du repère.
-
Puissance d’un nombre
Définition

\(\mathcal a\) est un nombre et \(\mathcal n\) un nombre entier positif.
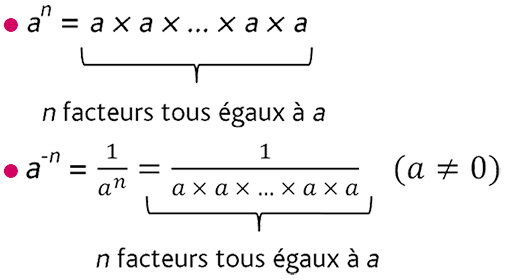
\(a^n\) est une puissance de \(\mathcal a\). \(\mathcal n\) s’appelle l’exposant et \(a^n\) se lit « \(\mathcal a\) exposant \(\mathcal n\) » ou « \(\mathcal a\) puissance \(\mathcal n\) ».
● \(a^0 = 1\;\;\;\left( {a \ne 0} \right)\)
● \(a^1 = a\)
● \(a^{-1} = \frac{1}{a}\;\;\;\left( {a \ne 0} \right)\)Exemples
● \(3^3 = 3 × 3 × 3 = 27\)
● \((–3)^2 = (–3) × (–3) = 9\)
● \(–3^2 =\;–3 × 3 =\;–9\)
● \(0,2^4 = 0,2 × 0,2 × 0,2 × 0,2 = 0,001 6\)
● \({\left( {\dfrac{3}{5}} \right)^2} = \dfrac{3}{5} \times \dfrac{3}{5} = \dfrac{9}{{25}}\)
● \({4^{- 2}} = \dfrac{1}{{{4^2}}} = \dfrac{1}{{16}}\)
● \(7^0 = 1\)
● \(7^1 = 7\)
Propriété

Quels que soient les nombres relatifs \(\mathcal a\) et \(\mathcal b\) non nuls et les nombres entiers \(\mathcal m\) et \(\mathcal n\) :
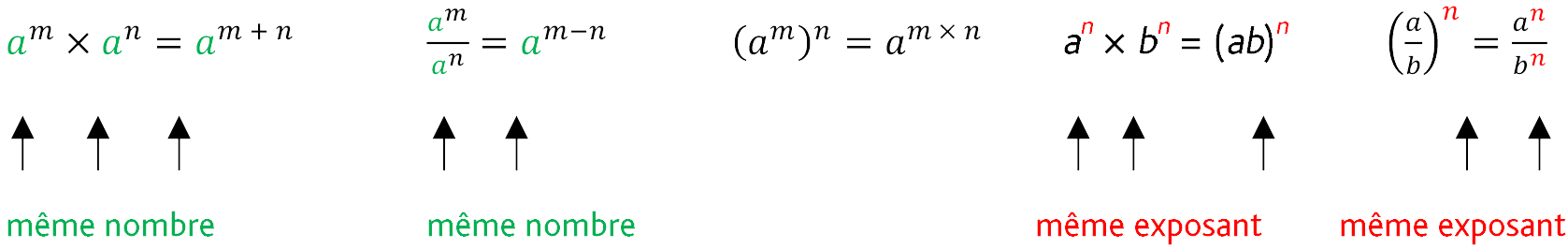
Exemples
● \(3^{–6} × 3^{2} = 3^{–6 + 2} = 3^{–4}\)
● \(\dfrac{{{4^5}}}{{{4^2}}} = {4^{5 - 2}} = {4^3}\)
● \((8^{–3})^2 = 8^{–3 × 2} = 8^{–6}\)
● \(4^6 × 5^6 = (4 × 5)^6 = 20^6\)
● \({\left( {\dfrac{{16}}{8}} \right)^3} = \dfrac{{{{16}^3}}}{{{8^3}}} = {2^3}\)
Règle de priorité

● En l’absence de parenthèses, on calcule les puissances avant d’effectuer les autres opérations (×, ÷, + et −).
● En présence de parenthèses, on effectue d’abord les calculs entre parenthèses.Exemples
● \(5 × 3^2 = 5 × 9 = 45\)
● \(−4^2 = −16\)
● \((5 + 3)^2 = 8^2 = 64\) -
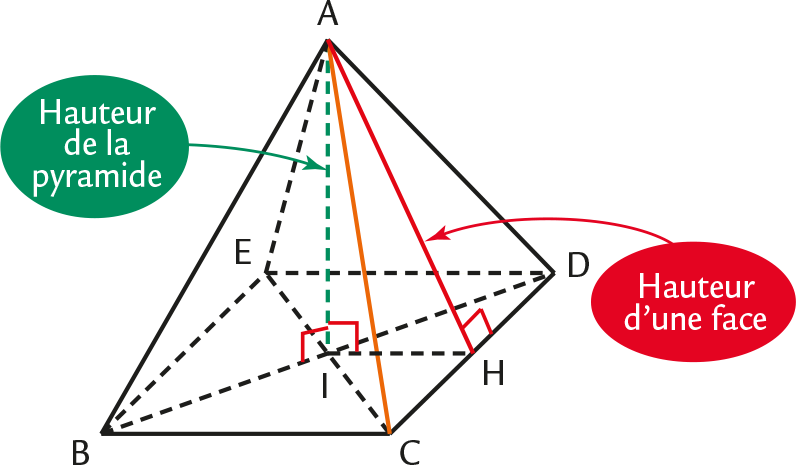
Pyramide
Définitions

● Une pyramide est un solide dont :
– une face est un polygone appelé base ;
– toutes les autres faces sont des triangles qui ont un sommet commun appelé sommet de la pyramide (ces faces sont appelées faces latérales de la pyramide).
● La distance entre le sommet de la pyramide et sa base est appelée hauteur de la pyramide.Exemple
La pyramide ABCDE est une pyramide à base carrée BCDE, de sommet A.
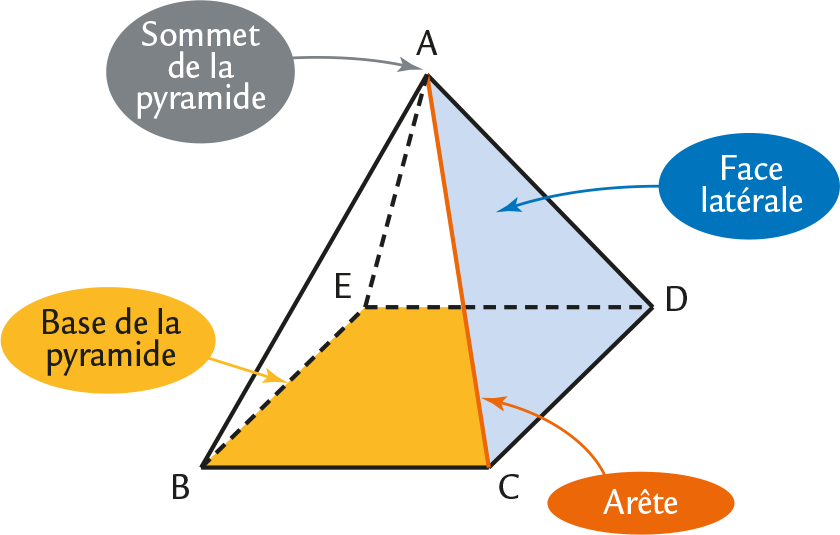
Remarque
Dans une pyramide, ne pas confondre la hauteur de la pyramide et la hauteur des triangles formant les faces latérales.